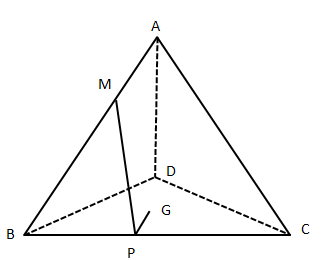
(单选题)如图，A—BCD是棱长为3的正四面体，M是棱上的一点，且MB=2MA，G是三角形BCD的重心，动点P在棱BC上，则PM+PG的最小值是：
A.
B.
C.3
D.
正确答案：B
解析
第一步，本题考查几何问题，属于立体几何类。
第二步，如图，将△BCD这一面沿BC边旋转与△ABC这一面在一个平面上，则PM+PG=MG，即为所求的最小值。
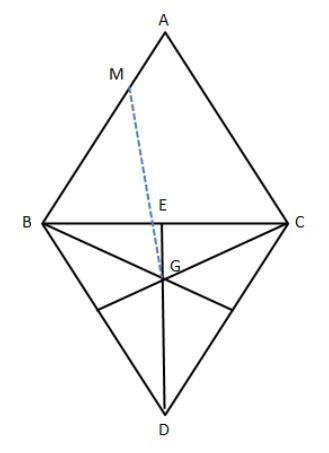
第三步，由于点G是△BCD的重心，可得
，
，则
，由MB=2MA，可知MB=2。
第四步，由于∠GBC=30°、∠ABC=60°，故∠GBM=90°，MG=
。
因此，选择B选项。
2024年公务员考试图书推荐
>>>2024版国家公务员录用考试专用教材（行测+申论）教材+真题4本
>>>【全新上市】2024第18版公务员考试行测+申论5100题12本
2024年公务员考试推荐课程
>>>【国省联报】2024年国考+省考公务员笔试《悦享班》第一期
扫码即可进入2024年公务员考试专属备考咨询平台，有疑问来这里
