在国考行测中,数量关系题最喜欢考和定最值问题,也是历来拉开考生差距的重要模块。
一、什么是和定最值问题
拿到一个题目,如何来判断一个题目是否属于和定最值问题,我们需要按以下两个条件去排除:
(1)几个数的和一定;(2)问题是求其中某个量的最大值或者最小值。

二、和定最值问题的题型特点
题干或问法中出现“最大或最小、最多或最少、至多或至少。”等,我们首先要考虑是和定值问题。
三、和定最值问题的解题原则及考点
1、正向最值问题:
(1)求最大量的最大值——让其他值尽量小。
(2)求最小量的最小值——让其他值尽量大。
2、逆向最值问题:
(1)求最大量的最小值——让各个分量尽可能的“均等”,且保持大的量仍大、小的量仍小。
(2)求最小量的最大值——让各个分量尽可能的“均等”,且保持大的量仍大、小的量仍小。
3、混合最值问题:
(1)求第 N 大的数的最大值
(2)求第 N 大的数的最小值
注意:求解混合最值问题的时候,需要利用正向最值和逆向最值的原则求解。
在数量关系模块中主要考查大家逆向最值和混合最值的掌握程度,所以我们在做题的时一定要注意题干中的限定条件,再进行求解。
【真题训练】
【例1】(2019国考省级以上试卷68题)花圃自动浇水装置的规则设置如下:
①每次浇水在中午12:00~12:30之间进行;
②在上次浇水结束后,如连续3日中午12:00气温超过30摄氏度,则在连续第3个气温超过30摄氏度的日子中午12:00开始浇水;
③如在上次浇水开始120小时后仍不满足条件②,则立刻浇水。
已知6月30日12:00~12:30该花圃第一次自动浇水,7月份该花圃共自动浇水8次,问7月至少有几天中午12:00的气温超过30摄氏度( )
A.18
B.20
C.12
D.15
【解析】正确答案为D。
根据题意,若要使7月份中午气温超过30摄氏度的天数尽可能少,则应同时满足两个条件:(1)超过30摄氏度的日子均以连续3天的方式出现;(2)未超过30摄氏度的日子均以连续120/24=5天的方式出现。
题干问“至少”,从最小的选项开始代入。
C项:若超过30摄氏度的日子有12天,则未超过30摄氏度的日子有31-12=19天。根据规则②可知,12天中浇水12/3=4次;根据规则③可知,19/5=3.8,即19天中浇水3次。4+3=7次,与“浇水8次”矛盾,排除;
D项:若超过30摄氏度的天数为15天,则未超过30摄氏度的天数为31-15=16天。根据规则②可知,15天中浇水15/3=5次;根据规则③可知,16/5=3.2,即16天中浇水3次,5+3=8次。满足题意。
【例2】(2019国考省级以上试卷73题)A和B两家企业2018年共申请专利300多项,其中A企业申请的专利中27%是发明专利,B企业申请的专利中,发明专利和非发明专利之比为8︰13。已知B企业申请的专利数量少于A企业,但申请的发明专利数量多于A企业。问两家企业总计最少申请非发明专利多少项( )
A.250
B.255
C.237
D.242
【解析】正确答案为C。
![]()
已知A企业申请的专利中27%是发明专利,即,则A企业申请的专利数为100的整数倍。又已知B企业申请的专利数量少于A企业,两者专利数量之和为300多,则A企业申请的专利为200项或300项。分类讨论:若A企业申请的专利为200项,则此时A企业的发明专利为200x27%=54项。根据B企业申请的发明专利数量多于A企业且B企业,说明B企业发明专利为8的整数倍且多于54,故B企业发明专利至少有56项,此时B企业非发明专利为项,因此两家企业申请非发明专利项数最少为200x(1-27%)+91=146+91=237;
![]()
若A企业申请的专利为300项,则此时A企业的发明专利为300x27%=81项。根据B企业申请的发明专利数量多于A企业且B企业,说明B企业发明专利为8的整数倍且多于81,故B企业发明专利至少有88项,相应的B的专利总数为项,则此时A、B企业的专利总数为531项,不满足总数为300多项,与题意矛盾,错误。
综上所述,两家企业申请非发明专利数最少为237项。
备注:实际考试中只需要算出第一种情况的结果为237项,对比选项发现237已经是选项中最少的结果了,故不可能有更小的情况,无需再讨论第二种情况。
【例3】(2019北京试卷84题)某次知识竞赛的决赛有3人参加,共有12道题。规则为每题由1人以抢答方式答题,其余2人不作答。每道题正确得8分,错误扣10分。如所有人均回答了问题,且得分均为正数,则3人得分之和的最小值()
A.低于10分
B.在10~15分之间
C.在16~20分之间
D.高于20分
【解析】正确答案为C。
![]()
设每人答对题目数量为x,答错题目数量为y,每人得分均为正数,则8x-10y>0,化简得:,要使3人得分之和最小,每人得分应尽量小,因此答对题目应尽量少。而x、y均为整数,得分均为正数,且答对加分低于答错扣分,因此每人答对题目比答错题目至少多1题。当x=y+1时,不同得分情况如下:
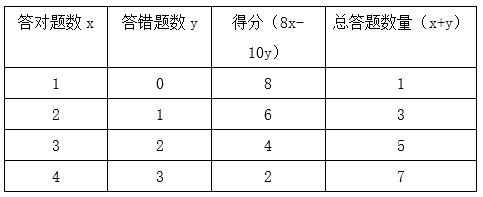
三人总答题数不大于12道,从1/3/5/7中任选三个数字组合(可重复),最多答题1+3+7或1+5+5或3+3+5,均为11道(这11道题的得分之和为8+6+2或8+4+4或6+6+4,均为16分),因此需要其中一人再多答对剩下的1题(得8分),此时三人总分最少为16+8=24分。
故正确答案为D。
备注:本题有争议。因题干未明确表示是否所有题目都有人回答,若允许存在未回答的题目,则得分最少的答题情况为:1+3+7或1+5+5或3+3+5,即3人共答11题,另有1题3人均未回答,得分之和最少为8+6+2分,则争议答案为C。
【例4】(2018国考地市级试卷67题)枣园每年产枣2500公斤,每公斤固定盈利18元。为了提高土地利用率,现决定明年在枣树下种植紫薯(产量最大为10000公斤),每公斤固定盈利3元。当紫薯产量大于400公斤时,其产量每增加n公斤将导致枣的产量下降0.2n公斤。则该枣园明年最多可能盈利多少元( )
A.46176
B.46200
C.46260
D.46380
【解析】正确答案为B。
当紫薯产量大于400公斤时,每增加n公斤将导致枣的产量下降0.2n公斤。
假设紫薯的产量为(400+n)公斤,则此时枣的产量为(2500-0.2n)公斤。
则总盈利为18x(2500-0.2n)+3x(400+n)=46200-0.6n,要让总盈利最大,则n取0,此时总盈利为46200元。














