工程问题是数量关系中最重要的也是最常见的一种题型,几乎所有的行测类的考试都会涉及,同时赋值法是我们解决工程问题最有力的工具,那么对于赋值类的工程问题做好以下四步,让你轻松得出答案。
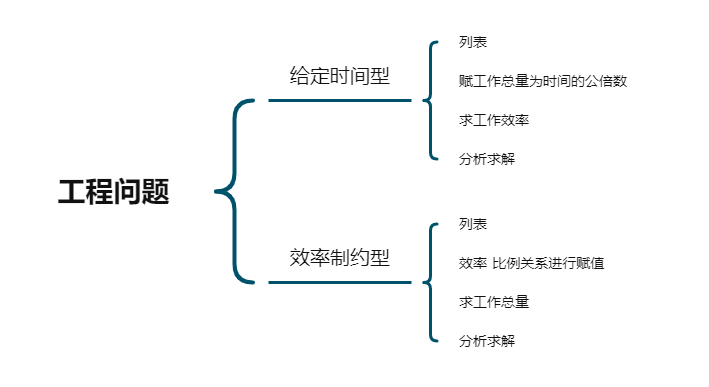
第一种类型题:给定时间型(题目中只给定工作时间时)
解题四步:1.列表2.赋工作总量为时间的公倍数3.求工作效率4.分析求解
【例1】(2020江苏)一项工程由甲、乙工程队单独完成,分别需50天和80天。若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成,则丙工程队单独完成此项工程所需的时间是:
A.40天
B.45天
C.50天
D.60天
【答案】D
【解析】
第一步:列表即为把材料中的已知数据填入咱们的工程问题的公式中。
工作总量=效率×时间
甲工程队50
乙工程队80
第二步:赋值工作总量,由于甲乙工程队是分别完成一项工程,工作总量相等,此时我们赋值工作总量为时间的公倍数,在这里50和80的公倍数我们选择其最小公倍数400。
工作总量=效率×时间
甲工程队40050
乙工程队40080
第三步:求效率,我们通过赋值已有工作总量为400,甲乙两队分别完成的时间为50天和80天,此时可分别求出甲乙两队的效率。
工作总量=效率×时间
甲工程队400850
乙工程队400580
第四步:分析求解,经过前三步我们以得知甲乙两队的工作总量、效率和时间,此时根据后续问题分析解决本题,若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成。
工作总量=(甲的效率+乙的效率)×20+(乙的效率+丙的效率)×12
400=(8+5)×20+(5+丙的效率)×12,解得丙的效率为20/3,故丙工程队单独完成需要400÷20/3=60天
第二种类型题:效率制约型(当题目中不仅给定工作时间,还给出与效率相关的某个逻辑关系时)
解题四步:1.列表2.效率比例关系进行赋值3.求工作总量4.分析求解
【例2】(2018四川)甲工程队与乙工程队的效率之比为4:5,一项工程由甲工程队单独做6天,再由乙工程队单独做8天,最后由甲、乙两个工程队合作4天刚好完成,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多多少天?
A.3
B.4
C.5
D.6
【答案】C
【解析】
第一步:列表即为把材料中的已知数据填入咱们的工程问题的公式中。甲队工作共4+6=10天,乙队工作共4+8=12天
工作总量=效率×时间
甲工程队10
乙工程队12
第二步:赋值效率,由于甲乙工程队是合作完成一项工作,甲工程队与乙工程队的效率之比为4:5,我们赋值甲乙两队的效率为4和5。
工作总量=效率×时间
甲工程队410
乙工程队512
第三步:求工作总量,我们通过赋值效率可以分别求出甲乙两工程队的工作总量
工作总量=效率×时间
甲工程队40410
乙工程队60512
故总的工作总量=甲工程队总量+乙工程队总量=40+60=100
第四步:分析求解,经过前三步我们以得知甲乙两队的工作总量、效率和时间,此时根据后续问题分析解决本题,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多多少天。
甲工程队单独完成所需时间:总的工作量÷甲的效率=100÷4=25
乙工程队单独完成所需时间:总的工作量÷乙的效率=100÷5=20
故则甲工程队所需天数比乙工程队所需天数多5天。
可以发现,对于赋值类的工程问题,只要按部就班通过上述四个步骤就能轻松得到答案。